Some projects I have worked on
I worked with Prof.Manuel Torres Labansat, studying the properties of topological solitons in potentials that have many local minima trapped between two global minima. We found that in many cases, the false vacuum pressure stabilizes the repulsive force between solitons, allowing for static multikink solutions. In addition, I simulated the collision between the multikinks of a modulated double sine-gordon potential we proposed. The generalization to higher-dimensional topological solitons arising in gauge theories and their interpretation is a potential research topic, and we have plans to work on it in the future. I presented this project at the AMC National Physics Congress, and there's an article in preparation for reporting our results.
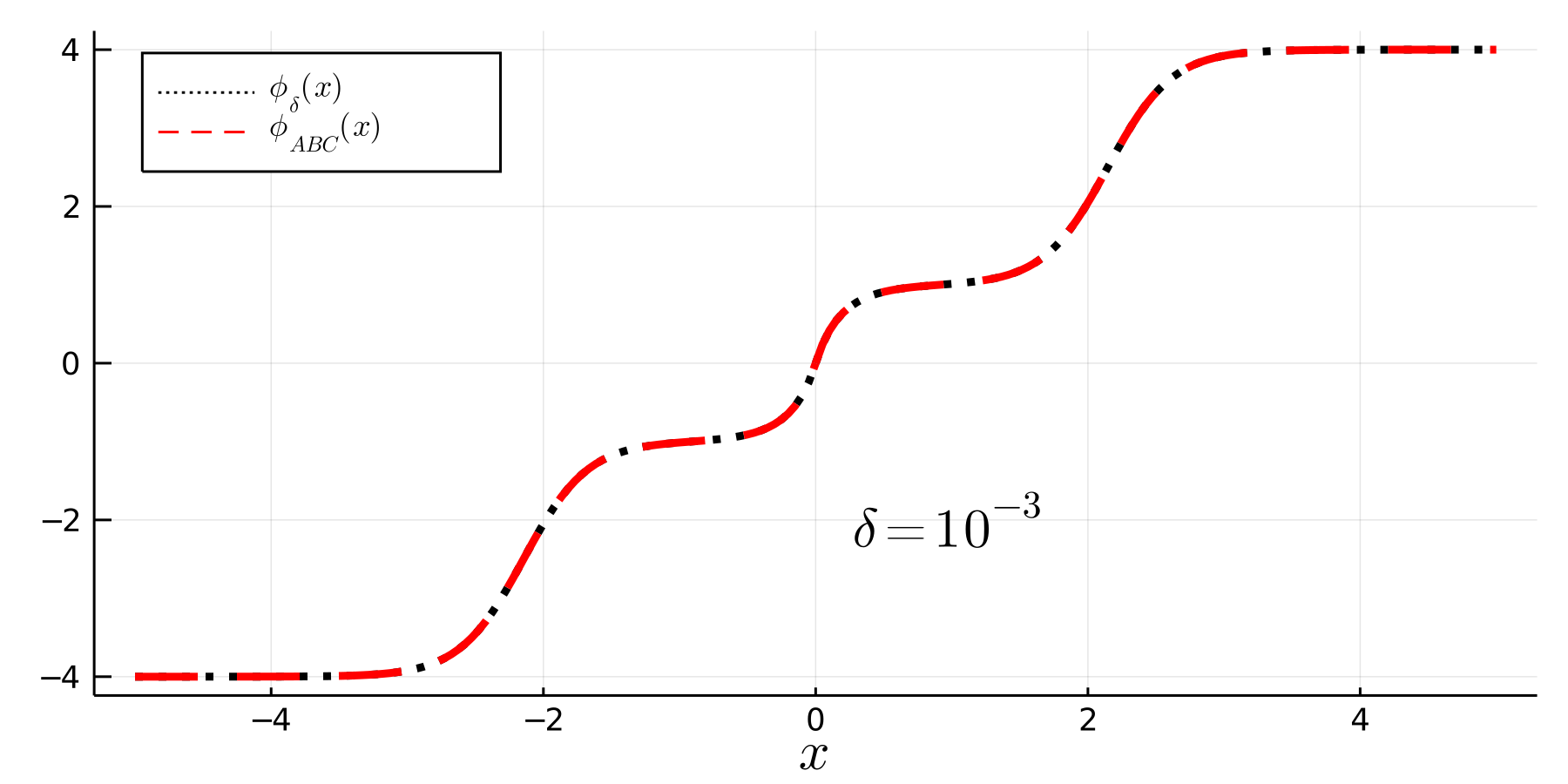
Due to the particle like properties of solitons, it's natural to ask whether they have a corresponding one-particle state in the quantum theory. In this project I quantized around the kink solutions of a generalized \(\phi^4\) potential which allowed for static multikink solutions. Given the non analytic behaviour of the potential, solving for the normal modes in the kink sector was highly non trivial. However, with a suitable transformation the eigenvalue equation can be cast as Pöschl–Teller Schrödinger equation. The force between interacting kinks was also calculated using asymptotic analysis. This project led to an article published in 2021.

While doing research for my BSc thesis I learned a really valuable lesson about how science advance. Sometimes when trying to answer a really hard question you end up answering another, sometimes easier, unexpected question (or many). That's how I arrived to one of my favorite articles, "The fate of the false vacuum" by Sidney Coleman.
It turns out that, in field theory, it's impossible for a system at a higher energy vacuum (false vacuum) to decay to a vacuum with lower energy (true vacuum) by standard means. An infinite amount of energy would be necessary to turn all the false vacuum into true vacuum at the same time in all space. However, Coleman theoreticized that in field theory the tunneling occurs through the nucleation of true vacuum bubbles which later expand at near \(c\) speed. Of special interest are the tunneling rates which are calculated by using Coleman's formalism. Coleman's formalism involves finding solutions to the non-linear field equations in Euclidian space, the solutions are an special kind of non-topological solitons called bounces.
While working with Prof. Manuel Torres Labansat on a generalized \(\phi^4\) model, we noticed that our model was adecuate to study the vacuum decay phenomenon. As a result we found a general set of virial relations that reproduce two well known results in scalar theories with vacuum decay and lead to more relations whose interpretation has still to be studied.

Can we have a well defined photon wave function in position space? Are Maxwell's equations already quantum? does the position operator make sense for photons?. Motivated by the above questions, I started my research journey.
This was my first research project, along the way, I constructed the photon wave function, found its wave equation, constructed the Hamiltonian and Spin operators, learned and applied representation group theory to further examine the transformation properties of the wave function, and, worked with the expected symmetries of the theory to prove they hold.